1884a(45)
Lecture 45. Du syllogisme
- Définition du syllogisme
- Le syllogisme
- Les termes
- Les propositions
- Mécanisme du syllogisme
- Explication algébrique du syllogisme
- Explication géométrique d'Euler
- Le syllogisme est un raisonnement purement formel
- Le principe du syllogisme est le principe d'identité
- Modes, figures, et formes du syllogisme
- Modes du syllogisme
- Elimination des modes faux
- Règles au moyen desquelles se fait cette élimination
- Figures du syllogisme
- Formes du syllogisme
- Raisonnements qui se ramènent au syllogisme
- Modes du syllogisme
- Conclusion -- Le syllogisme n'est-il qu'une tautologie
- Théorie de Stuart Mill
- Réfutation
Lecture 45. Du syllogisme
Nous avons vu en psychologie qu'il y avait deux formes de raisonnement: la déduction et l'induction. Nous allons étudier la première.
La forme la plus parfaite du raisonnement déductif est le syllogisme. C'est par lui que l'on conclut, d'une proposition reconnue pour vraie, à la vérité d'une proposition nouvelle. Ainsi, soit la proposition à prouver Paul est mortel, nous l'établissons en la déduisant d'une autre proposition reconnue pour vraie, Tous les hommes sont mortels, au moyen d'une proposition intermédiaire Paul est un homme. Le syllogisme complet a la forme suivante:
Tous les hommes (M) sont mortels (T);
Or, Paul (t) est un homme (M);
Donc, Paul (t) est mortel (T).
La dernière proposition renferme deux termes et l'attribut y a une extension plus grande que le sujet. Il s'appelle à cause de cela grand terme (T). Le sujet porte au contraire le nom de petit terme (t). Enfin dans les deux premières propositions se trouve un terme commun, auquel sont comparés tour à tour les deux termes déjà examinés; ce terme est nommé moyen terme (M).
La troisième proposition d'un syllogisme porte le nom de question ou de conclusion, suivant qu'on l'envisage avant ou après la démonstration. Les deux premières propositions sont les prémisses. Celle où le grand terme est comparé au moyen se nomme majeure, celle où se trouve le petit, mineure.
Etudions maintenant le mécanisme du syllogisme. Il a pour objet de démontrer la question ou conclusion. Or, toute proposition comprend deux termes: un sujet, un attribut affirmé de ce sujet; si, pour être établie, la proposition demande démonstration, c'est qu'on ignore si ces deux termes se conviennent. Pour le savoir, on cherche un troisième terme qui permette de décider. Il faut démontrer que T contient t--au point de vue de l'extension, bien entendu--ce que nous pouvons écrire T > t. Pour cela, comparons T à M. Nous trouvons que M est contenu dans T. On a T > M (Les hommes sont compris dans la classe des êtres mortels). Comparons maintenant M à t. On trouve M > t (Paul est compris dans la classe des hommes). Nous avons, d'une part T > M, de l'autre M > t; d'où l'on tire T > M > t; T > t (Paul est compris dans la classe des êtres mortels).
Telle est la théorie du syllogisme au point de vue de l'extension. Si l'on voulait en faire la théorie au point de vue de la compréhension, il n'y aurait qu'à renverser l'ordre des inégalités précédentes. Il suffit pour le voir de se rapporter à la loi: L'extension est en raison inverse de la compréhension. Ainsi, si au point de vue de l'extension T > t, au point de vue de la compréhension on a t > T. Il est évident que le nombre des caractères qui définissent Paul est plus grand que le nombre de caractères qui définissent mortel.
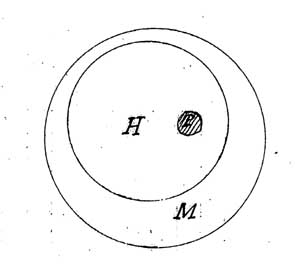
Dans ses Lettres à une princesse d'Allemagne, Euler a exposé une théorie fort ingénieuse du syllogisme: il représente par un cercle l'extension de chacun des trois termes du syllogisme; leur rapport de convenance ou de disconvenance est indiqué par le rapport de contenance ou d'extériorité de ces cercles.
Représentons par le cercle H l'idée d'homme, par le cercle M l'idée
de mortel, enfin par le cercle P l'idée de Paul. H est contenu
dans M (tous les hommes sont mortels); de plus P est contenu dans
H (Paul est un homme). Il suffit de regarder la figure pour voir
que P est contenu dans M (Paul est mortel).
Si le syllogisme au contraire était présenté sous la forme:
Nul homme n'est immortel;
Or, Paul est un homme;
Donc, Paul n'est pas immortel,
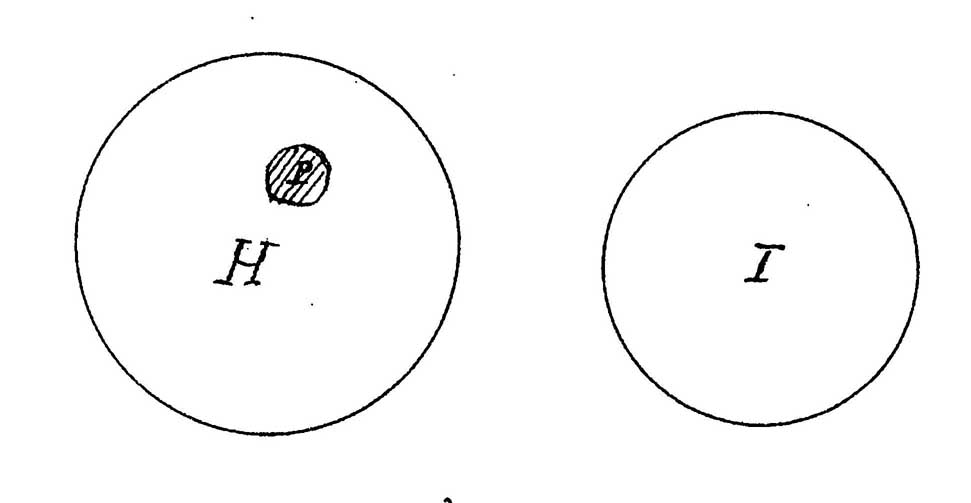
on aurait en désignant homme, immortel, Paul, par les cercles
H, I, P, la figure suivante, d'après la méthode d'Euler:
Ce qui montre immédiatement que P est extérieur à I: l'idée d'immortel ne convient donc pas à l'idée de Paul.
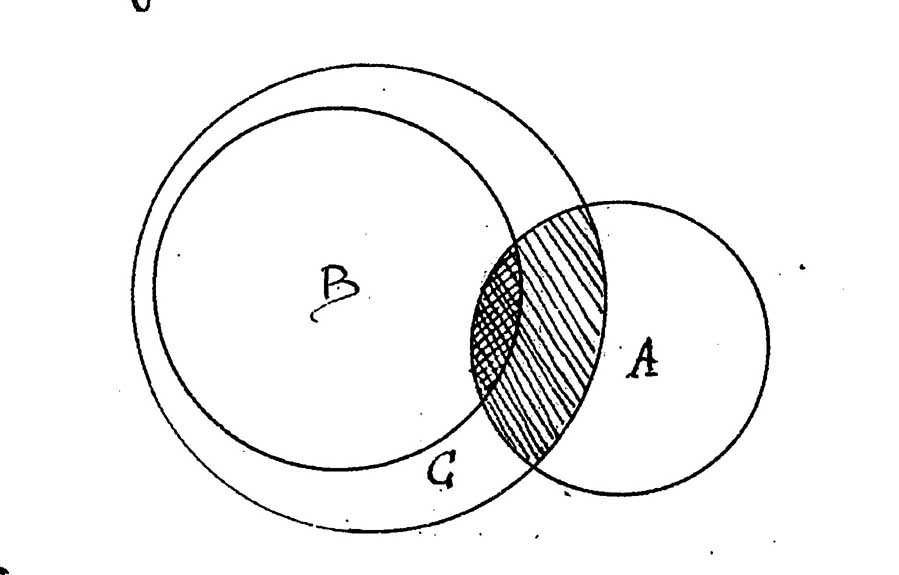
Soit le syllogisme général:
Quelque A est B;
Tout B est C;
Donc, quelque A est C
on le figurerait ainsi:
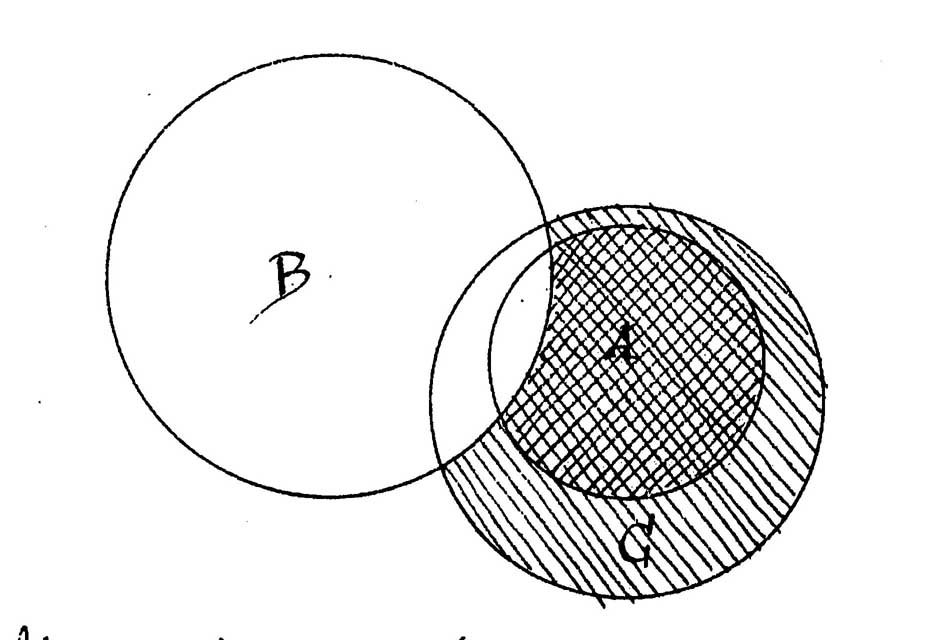
Soit encore le syllogisme contraire:
Quelque A n'est pas B
Tout A est C
Donc, quelque C n'est pas B
On aurait:
Cette figuration a l'avantage de bien faire comprendre quelle est l'essence du syllogisme. Ce n'est pas de comparer des quantités inégales comme semble le faire voir la figuration algébrique que nous avons indiquée plus haut, mais de marquer un rapport de contenant à contenu. De plus, cette méthode montre nettement que le syllogisme est purement formel. Mettez telles propositions qu'il vous plaira à la place des lettres des exemples précédents, le syllogisme en lui-même n'en sera pas moins rigoureux, quand bien même les prémisses seraient fausses, quand bien même elles n'auraient aucun sens. Voici pour le prouver, divers exemples de syllogismes qui, en eux-mêmes, sont parfaitement exacts, et qui, figurés par la méthode d'Euler, donneraient trois cercles concentriques représentant le plus grand, le grand terme; le second, le moyen terme; le troisième, le petit terme. Comme syllogismes, ils sont donc irréprochables et n'en sont pas moins faux, soit dans leurs prémisses, soit dans leurs conséquences.
Le premier énonce trois propositions fausses:
Tout sentiment courageux est louable;
Or, l'imprudence est un sentiment courageux;
Donc, l'imprudence est louable.
Cet autre de deux prémisses fausses tire une conclusion vraie:
Ma tabatière est dans la lune;
La lune est dans ma poche;
Donc ma tabatière est dans ma poche.
Le troisième se compose de deux prémisses vrais, d'une conclusion fausse:
Tout rat mange du lard;
Or, rat est une syllabe;
Donc, une syllabe mange du lard.
Nous verrons plus loin la cause qui peut faire tirer de deux prémisses vraies une conclusion fausse. Ces exemples n'en démontrent pas moins combien le syllogisme est formel.
Quel est le principe qui préside au mécanisme du syllogisme? C'est le principe d'identité. En effet, la conclusion y est conçue comme comprise dans les prémisses; elle est vraie, parce qu'elle est identique à une partie des prémisses admises comme vraies.
Les modes du syllogisme dépendent de la quantité et de la qualité des propositions composantes. Or nous avons vu qu'il y avait quatre sortes de propositions à ce double point de vue, et avons vu qu'elles étaient désignées par les lettres A E I O. On a calculé qu'elles pouvaient se combiner de 64 façons différentes. Il y aurait alors 64 modes de syllogisme. Mais en appliquant un certain nombre de règles générales auxquelles doit se conformer un syllogisme pour être juste, on trouve que 54 de ces modes sont faux. Il n'en reste dès lors que dix possibles.
Ces règles du syllogisme, dont nous venons de parler, étaient selon l'Ecole qui les énonçait en vers au nombre de 7. Hamilton en a réduit le nombre à 3:
- Tout syllogisme doit avoir trois termes, et rien que trois termes. Le corollaire de cette loi est qu'un mot n'y saurait être pris dans deux sens différents: car cela équivaudrait à l'introduction d'un quatrième terme.
- La majeure doit être universelle et la mineure affirmative. Tout d'abord, la majeure doit être universelle. En effet, s'il n'en était pas ainsi, le moyen terme pourrait ne pas avoir dans la mineure la même extension que dans la majeure, ce qui vicierait le raisonnement. Ainsi, le syllogisme suivant serait inexact:
Certains ouvrages d'art ont la forme cubique;
Or, un tableau est un ouvrage d'art;
Donc, un tableau a la forme cubique.
En outre, la mineure doit être affirmative; en effet elle énonce l'application à la question présente de la règle générale fournie par la majeure. Elle doit donc affirmer qu'elle convient à cette question. C'est par cela qu'on ne saurait employer sans erreur un syllogisme de la forme de celui-ci:
Tout homme est un animal;
Or, nul cheval n'est homme;
Donc, nul cheval n'est animal.
- La conclusion doit s'accorder en quantité avec la mineure, en qualité avec la majeure. En effet, d'abord, la conclusion a pour sujet le petit terme, et le grand pour attribut. Mais comme leur relation entre eux est déterminée par leurs relations avec le moyen terme, et que celui-ci est comparé avec le grand terme dans la majeure, la mineure devant d'autre part être toujours positive, il s'ensuit nécessairement que la conclusion devra toujours être positive si la majeure est positive, négative si elle est négative.
En outre, le petit terme, dans la mineure, est affirmé comme contenu dans le moyen terme. Or, dans la conclusion, le grand terme ne peut être attribué à un plus grand nombre d'individus que n'en contient le moyen terme. Donc, si l'une de ces propositions est particulière, l'autre devra l'être aussi; universelle au contraire, si elle est universelle.
Le syllogisme peut prendre différentes figures. Elles dépendent de la place qu'occupe le moyen terme dans les prémisses. Il peut être attribut dans la majeure et dans la mineure, sujet dans toutes les deux, attribut dans la première et sujet dans la seconde, et vice versa. On peut donc distinguer ainsi quatre figures de syllogismes.
Le syllogisme type que nous avons indiqué est susceptible de changements qui l'abrègent ou le complètent. Les différentes formes qu'il peut revêtir ainsi sont ce qu'on nomme les différentes espèces de syllogisme.
Les syllogismes "hypothétiques" sont ceux où la majeure conditionnelle contient la conclusion:
S'il y a un Dieu, il faut l'aimer;
Or, il y a un Dieu;
Donc, il faut l'aimer.
Dans ce syllogisme, la majeure se divise en deux parties: la première est l'antécédent, la deuxième le conséquent.
Les syllogismes "disjonctifs" sont ceux où la prémisse proposition pose une alternative.
Ceux qui ont tué César sont ou parricides ou défenseurs de la
liberté;
Or, ils ne sont pas parricides;
Donc, ils sont défenseurs de la liberté.
Il faut dans ce cas que la division soit exacte et complète et que la première proposition énumère tous les cas possibles. Une disjonction est fausse quand on a omis un terme.
Le raisonnement peut encore revêtir d'autres formes, mais qui toutes peuvent se ramener au syllogisme.
- L'Enthymème, syllogisme dont une proposition est sous-entendue: Plus d'amour, partout plus de joie.
- L'Epichérème, syllogisme où une ou deux prémisses sont accompagnées de leurs preuves. Tel est par exemple, le Pro Milone: Il est permis de tuer celui qui nous dresse des embûches: preuves, Clodius a voulu faire périr Milon dans un guet-apens: preuves, Milon a eu le droit de tuer Clodius.
- Le Prosyllogisme, argument composé de deux syllogismes, tels que la conclusion du premier devient la majeure du second. On peut faire aussi un prosyllogisme composé de plusieurs syllogismes, tels que la conclusion de chacun d'eux devienne la majeure du suivant.
- Le Sorite est un polysyllogisme, argument composé d'un nombre indéterminé de propositions liées entre elles, de telle sorte que l'attribut de la première soit le sujet de la seconde, le sujet de la seconde l'attribut de la troisième, et ainsi de suite, la conclusion unissant le sujet de la première à l'attribut de la dernière.
Tel est le raisonnement suivant, prêté par Montaigne à un renard qui avant de passer la glace, écoute et entend le bruit de l'eau:
Ce qui fait du bruit remue;
Ce qui remue n'est pas gelé;
Ce qui n'est pas gelé est liquide;
Ce qui est liquide plie sous le faix;
Donc cette rivière qui fait du bruit pliera sous le faix.
- Le Dilemme a pour majeure une disjonctive de deux membres et dans laquelle
on conclut par rapport au tout ce qu'on avait déjà conclu par
rapport à chaque partie de la disjonctive. Tel est le raisonnement
que faisait un ministre anglais, pour exiger de l'argent des évêques:
Si tu dépenses beaucoup, tu es riche; tu dois payer;
Si tu ne dépenses rien, c'est que tu fais des économies; paye encore.
Quelle est la valeur du syllogisme? A l'époque de la scolastique, le syllogisme est l'instrument presque unique des philosophes. La Renaissance commence une réaction contre lui: Bacon et Descartes l'attaquent vivement. De nos jours, Stuart Mill a cherché lui aussi à diminuer la valeur du syllogisme. Il n'apprend rien, dit-il, puisqu'il n'y a rien de plus dans la conclusion que dans les prémisses; tout syllogisme se réduit, en fin de compte, à une tautologie. L'induction a seule une valeur logique, car seule elle peut nous fournir les principes de la déduction: quand on affirme que tous les hommes sont mortels, on affirme virtuellement que Paul est mortel. Le syllogisme, qui ne sert qu'à dégager cette seconde proposition de la première, ne donne donc rien de nouveau.
Toutefois [crossed out: bien qu'incontestablement on ne lui doive rien] bien qu'il soit par lui-même tout formel et insuffisant, il est autre chose qu'une pétition de principe ou une tautologie. Sans doute la conclusion est dans les prémisses. Mais elle n'y est qu'en puissance; il faut l'en dégager: c'est l'oeuvre du syllogisme: il lie en moi deux idées qui auparavant n'étaient pas attachées; en ce sens au moins, il fait donc connaître quelque chose de nouveau. D'ailleurs, son importance est suffisamment établie pour les sciences mathématiques: chacune d'elle est un immense prosyllogisme, et, à moins de nier leur utilité, et de prétendre qu'il n'y a rien de plus dans les formules les plus élevées auxquelles elles arrivent que dans les quelques définitions qui leur servent de base, il faut bien reconnaître l'utilité du raisonnement syllogistique.